The Lagrangian points are locations in space in the vicinity of two orbiting masses where the gravitational forces and the orbital motion balance each other to form a point at which a third body of negligible mass would be stationary relative to the two bodies.
There are a number of web resources describing the Lagrangian points, some of them offering a very good introduction and description of the 5 Lagrangian points, while others insist on the techical aspects of the problem. Nonetheless, in the following article we'll try to add to the non-mathematical and intuitive descriptions available on the web (like, for instance, the
ESA page related to the 5 lagrangian points or the
Wikipedia article) a detailed-mathematical view of the problem, starting from the technical defintion which states that the Lagrangian points are the stationary solutions of the circular restricted three-body problem.
If we consider the restricted 3 body problem:
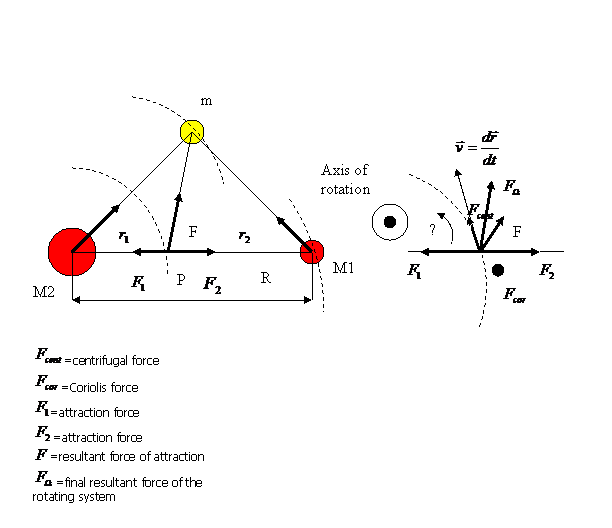
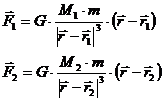
Considering an equilibrium point P we have the condition:
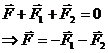
Then the resultant force is:
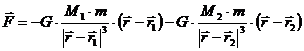
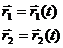
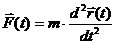
If we introduce the center of mass of a system like being a specific point where the system’s mass behaves as the system is concentrated in that specific point we will have the following relation:
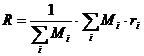
For the particular Sun-Earth system the barycenter is located as following:
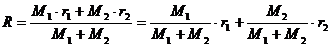
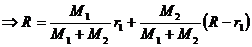
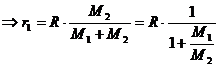
In the case 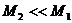 we have
we have 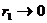 (449 km for the Sun-Earth system)
(449 km for the Sun-Earth system)
Now let’s introduce in the system the Coriolis force and the centrifugal force.
Coriolis force:
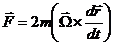
Centrifugal force:
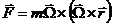
Then the resultant force is:
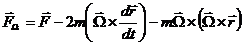
Correspondingly, the generalized potential is:
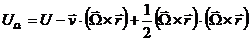
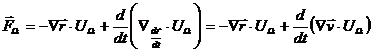
The first term from the formula above 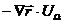 determines the position of the equilibrium points, and the second one
determines the position of the equilibrium points, and the second one 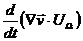 determines the stability of motion about the equilibrium points.
determines the stability of motion about the equilibrium points.
If we consider a Cartesian coordinates system around the center of mass of the system Sun-Earth as in the following picture:
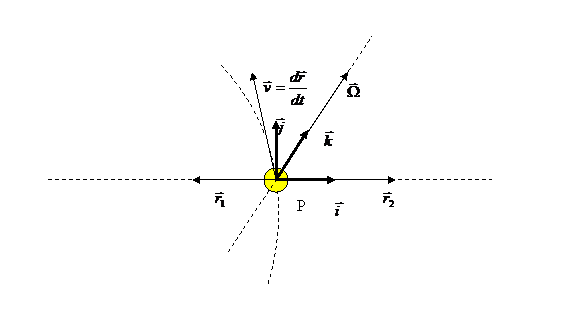
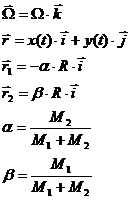
Considering all above we obtain the resultant force:
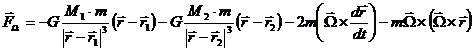
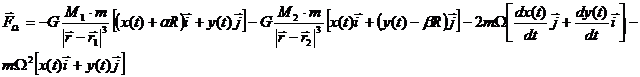 In order to determine the static equilibrium points we put the condition
In order to determine the static equilibrium points we put the condition
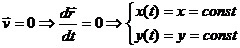
Then the resultant force became:
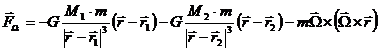
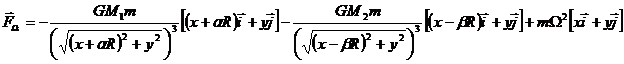
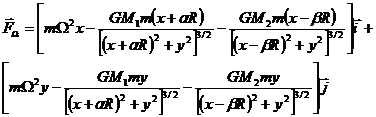
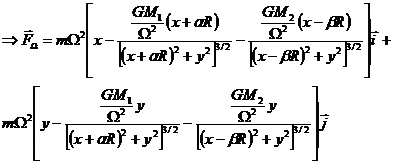
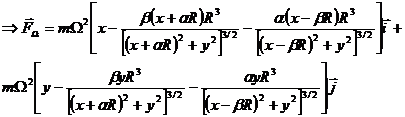
From the condition 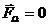 we will find the position of the equilibrium points.
we will find the position of the equilibrium points.
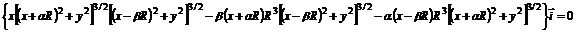
In particular, if we consider 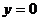 we can find the first 3 Lagrange points (located in the line Sun-Earth).
we can find the first 3 Lagrange points (located in the line Sun-Earth).
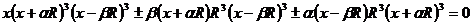
Now, in order to simplify the calculation we consider:
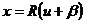
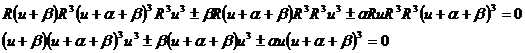
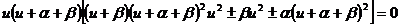
Let’s replace in the above formula the fact, that 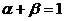 .
.
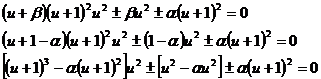
Now we have basically three possibilities (the fourth case is practically impossible):
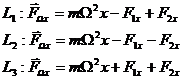
Correspondingly to the above cases we will have three equations:
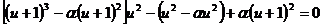 (1)
(1)
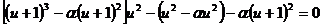 (2)
(2)
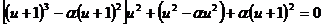 (3)
(3)
Or if we want to express the equations in a general form we can write:
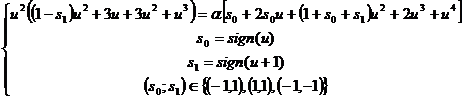
Then the three particular cases become:
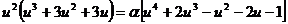 (1)
(1)
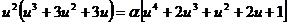 (2)
(2)
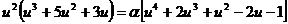 (3)
(3)
We have now to solve these 3 equations. We can do this either by using an approximation considering the particularity of the system Earth-Sun 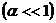 or we can solve it numerically using the Newton method.
or we can solve it numerically using the Newton method.
Let’s first consider the approximation 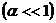 and try to find a series which approximate the real solution.
and try to find a series which approximate the real solution.
We then have in the first equation:
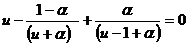
If we note 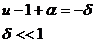
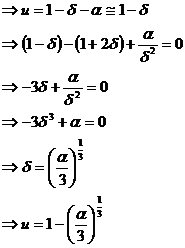
For the second equation we have:
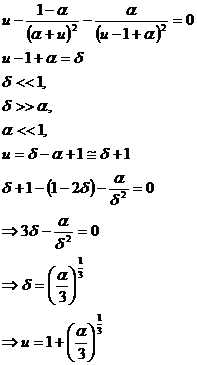
For the third equation:
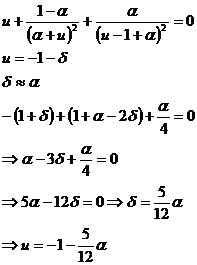
In the second case can be proven that the three equations have all just one real solution the other 4 being complex. The real solutions can be found being in the interval:
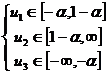
Using a numerical program and replacing the constants in the particular case of the system Earth-Moon-Sun we will have:
M1=1.98892E30;//mass of Sun [kg]
M2=5.9742E24;//mass of Earth [kg]
M3=7.36E22;//mass of Moon [kg]
R=1.4959610E8;//1 AU=R [km];
al=(M2+M3)/(M1+M2+M3);//alpha
be=M1/(M1+M2+M3);//beta
Then the roots of the three equations (calculated with a precision of 1e-14) are:
x1=-0.0100113196805154
x2=0.010078587510165
x3=-0.0100332069481937
So the physical coordinates of the first three Lagrange points of the system Earth-Moon-Sun are:
L1x=148097990.737622
L1y=0
L2x=151103362.50271
L2y=0
L3x=148094716.487738
L3y=0
expressed in km from the center of mass of the system.
In the particular case of the L2 point which will focus on we found it at 1507717.38502939 km from Earth on the line which lies the Sun and the Earth.
Let’s find now the solutions for the other 2 Lagrange points.
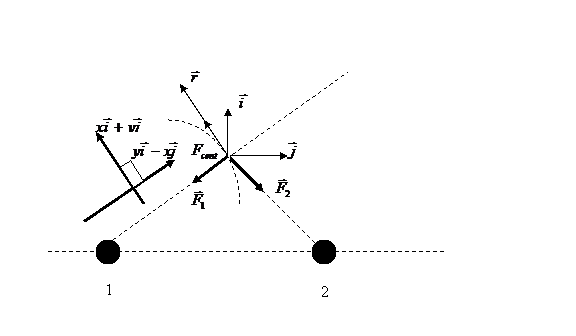
We have the resultant force:
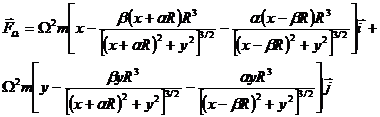
Considering the two directions (parallel 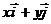 and perpendicular
and perpendicular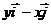 ) we obtain the projection on the perpendicular direction
) we obtain the projection on the perpendicular direction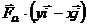 :
:
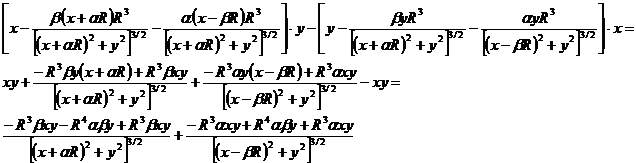
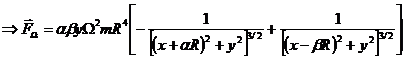
If 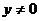 and
and 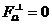
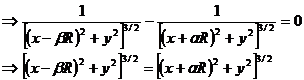
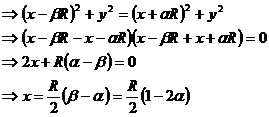
Let’s consider now the projection on the parallel direction:
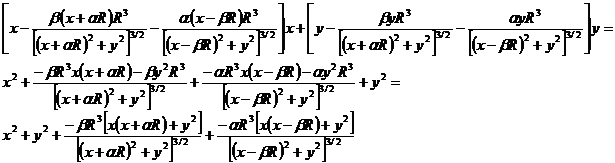 Replacing the previous solution
Replacing the previous solution 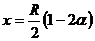
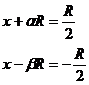
we have:
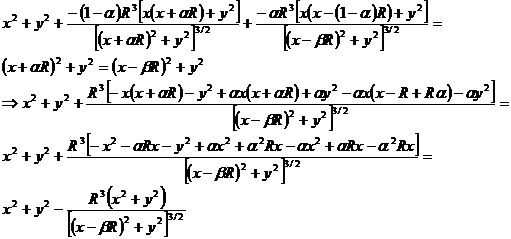
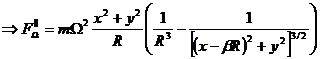
From the condition 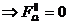
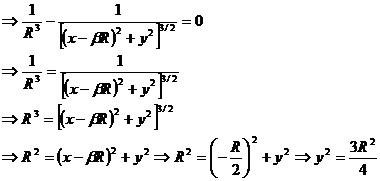
So the two solutions are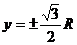 .
.
Then the last two Lagrange points are located as:

Physically the solutions are found replacing the constants for the system Earth-Moon-Sun
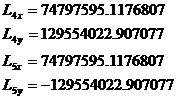
expressed in kilometers from the center of mass of the system.
Lissajous orbits around L2 point
We have to find the general solution of the system of equations around L2 point:
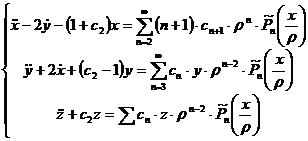
with:
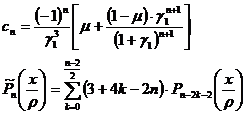
The general solution of the above system of equations can be proven to be of the form:
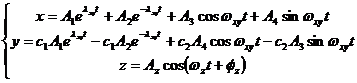
where,
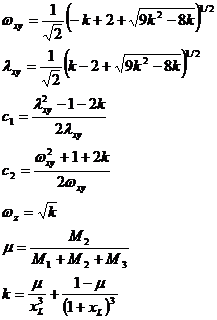
where 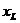 is the solution of the equation which gives us the L2 point.
is the solution of the equation which gives us the L2 point.
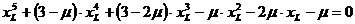
Based on the initial conditions the coefficients can be found as:

where:
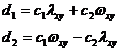
We can simplify the system of equations:
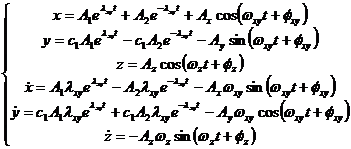
If we put the supplementary condition 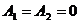 we obtain a Lissajous orbit in the liniarized restricted three body problem:
we obtain a Lissajous orbit in the liniarized restricted three body problem:
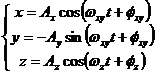
with 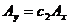 .
.
If 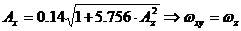 we obtain a Halo orbit around L2.
we obtain a Halo orbit around L2.
The following pictures show a typical Lissajous orbit with the conditions:
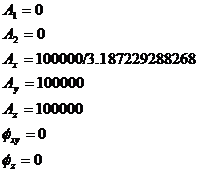
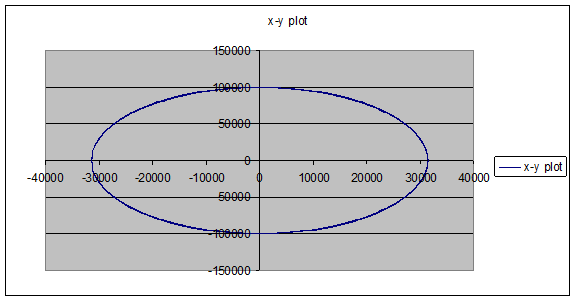
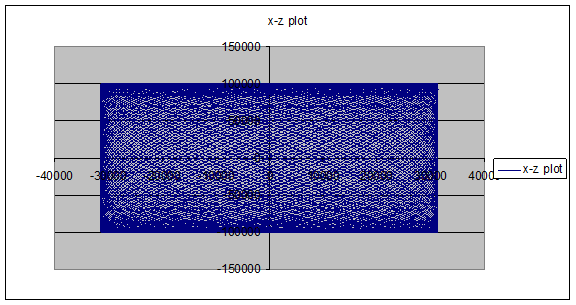
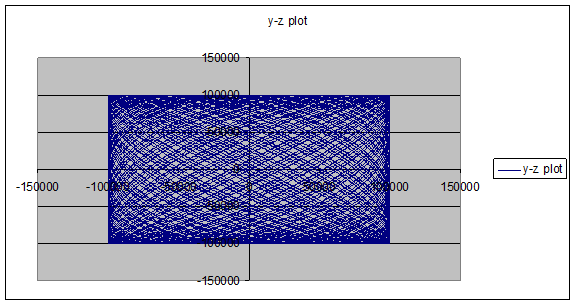
The following pictures show a general Lissajous orbit:
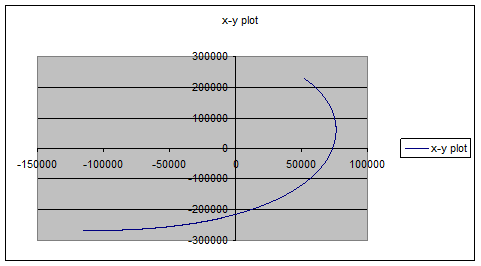
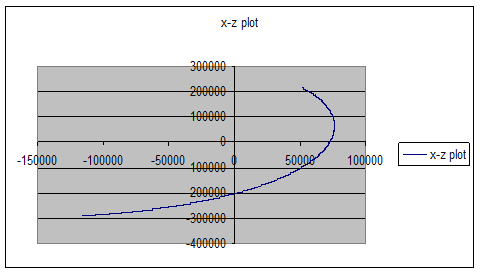
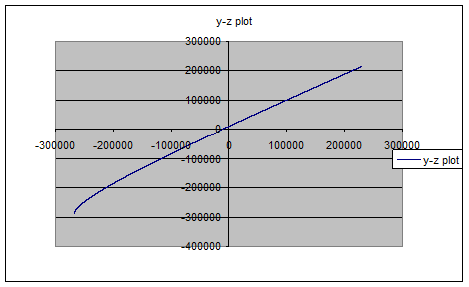
As can be seen, the exponential part of the equations results in a very fast grow of the orbit and, as consequence, the satellite will escape from the desired orbit. In conclusion the satellite should be kept in a liniarised Lissajous orbit such that the exponent is null.